문제
문제
시골에 있는 태양이의 삼촌 댁에는 커다란 참외밭이 있다. 문득 태양이는 이 밭에서 자라는 참외가 도대체 몇 개나 되는지 궁금해졌다. 어떻게 알아낼 수 있는지 골똘히 생각하다가 드디어 좋은 아이디어가 떠올랐다. 유레카! 1m^2의 넓이에 자라는 참외 개수를 헤아린 다음, 참외밭의 넓이를 구하면 비례식을 이용하여 참외의 총개수를 구할 수 있다.1m^2의 넓이에 자라는 참외의 개수는 헤아렸고, 이제 참외밭의 넓이만 구하면 된다. 참외밭은 ㄱ-자 모양이거나 ㄱ-자를 90도, 180도, 270도 회전한 모양(┏, ┗, ┛ 모양)의 육각형이다. 다행히도 밭의 경계(육각형의 변)는 모두 동서 방향이거나 남북 방향이었다. 밭의 한 모퉁이에서 출발하여 밭의 둘레를 돌면서 밭경계 길이를 모두 측정하였다.
1m^2의 넓이에 자라는 참외의 개수와, 참외밭을 이루는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지나는 변의 방향과 길이가 순서대로 주어진다. 이 참외밭에서 자라는 참외의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 K(1m^2당 자라는 참외의 개수)
둘째 줄부터 일곱번째 줄까지 방향, 길이
출력
밭에서 자라는 참외의 개수
풀이
처음에 생각을 해봤을 때, 어차피 육각형 고정이고 무조건 반시계 방향으로 밖에 갈 수 없으니 제일 큰 사각형에서 작은 사각형을 빼는 식으로 구현해야겠다고 생각했다. 같은 방향으로 가는 값들을 전부 합치면 무조건 그 전체 가로/세로 길이가 나오는데, 여기서 전체값이 아닌 작은 값으로 나눠진 입력 값들 중 꺾여지는 부분을 빼는 걸로 생각했다.
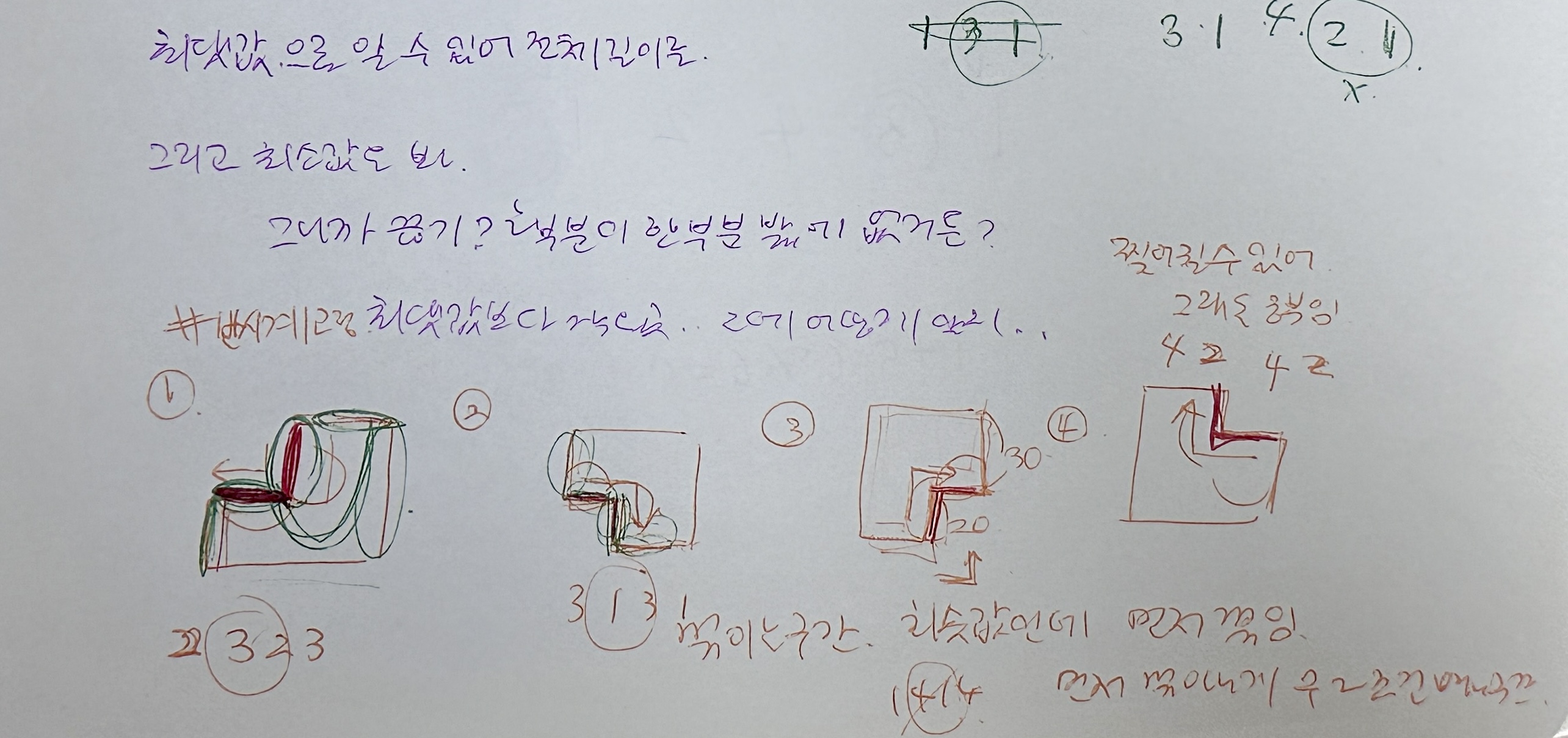
혼자 이해하려고 작성해본 거라 글씨체가 개판이지만... 이해를 위해 첨부해둔다.
그러니까 중간에 무조건 2323, 3131, 1414, 4242 이렇게 겹치는 부분이 무조건 생길 수 밖에 없는데 이 중 가운데 두 부분 2323의 값을 곱해서 빼버리면 된다. 만약에 앞뒤로 쪼개질 수도 있는데, 그래도 중간 부분만 곱하면 된다. 그니까 3...232 이런 식으로.
그래서 이렇게 풀어봤다.
🚧 틀린 코드 🚧
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int K = Integer.parseInt(br.readLine());
int result = 0;
int[] list = new int[5];
for(int i=1; i<5; i++) {
list[i] = 0; // 초기화
}
int min = 1; // 뺄 값
int prev = 1; boolean flag = false;
for(int i=0; i<6; i++) {
st = new StringTokenizer(br.readLine());
int drc = Integer.parseInt(st.nextToken());
int dis = Integer.parseInt(st.nextToken());
if(list[drc] == 0) {
list[drc] = dis;
prev = dis;
} else if(!flag) {
min = dis * prev;
flag = true;
}
}
result = Math.max(list[1], list[2]) * Math.max(list[3], list[4]);
bw.write((result-min)*K + "\n");
bw.flush();
bw.close();
br.close();
}
}prev 변수에 전 값을 저장해두고, 입력을 받았는데 이미 받은 값이 있다 = 겹치는 값에 해당한다. 그러면? min(뺄 값, 작은 직사각형)에 현재 값과 전 값을 곱하고, flag = true로 변경해둔다.
근데 이렇게 하면 값이 쪼개질 때 문제가 된다.
3 20
1 100
4 50
2 160
3 30
1 60
이런 입력을 받으면, 밑줄 친 부분을 곱해야 하는데, 30과 160(전 값이므로)를 곱하게 된다.
순서를 저장해둘 필요가 있어 drc 배열, dis 배열을 따로 만들어두고 순서대로 저장했다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st;
int K = Integer.parseInt(br.readLine());
int result = 0;
int min = 1; // 뺄 값
int len = 0, wid = 0;
int[] drc = new int[6];
int[] dis = new int[6];
for(int i=0; i<6; i++) {
st = new StringTokenizer(br.readLine());
drc[i] = Integer.parseInt(st.nextToken());
dis[i] = Integer.parseInt(st.nextToken());
if(drc[i] == 1 || drc[i] == 2) {
wid = Math.max(wid, dis[i]);
} else {
len = Math.max(len, dis[i]);
}
}
for(int i=0; i<6; i++) {
if(drc[(i+5)%6] == drc[(i+1)%6]) {
if(drc[(i+2)%6] == drc[i]) {
min = dis[i] * dis[(i+1)%6];
} else {
min = dis[i] * dis[(i+5)%6];
}
}
}
result = (wid * len)- min;
bw.write((result)*K + "\n");
bw.flush();
bw.close();
br.close();
}
}wid와 len은 최댓값으로 구해서 저장해두었다.
(i+5)%6은 사실상 (i-1+6)%6으로, 전 인덱스의 값을 찾는 값이고 (i+1)%6은 다음 인덱스의 값이다. 6으로 나누어 5번째 인덱스의 다음 인덱스를 0으로 인식하게 하였다.
만약 전 인덱스의 방향과 다음 인덱스의 방향이 동일하면, 1313 중에 중간의 3, 혹은 중간의 1에 해당하게 된다. 이 때 앞의 1을 곱할지 뒤의 1을 곱할지를 결정해야 한다. 이를 분별하기 위해 (i+1)%6의 다음 인덱스인 (i+2)%6의 값을 확인한다. 만약 이 (i+2)%6 인덱스의 방향이 현재 방향 값과 동일하다면 중간에 낀 값이므로 곱하면 된다.
문제를 풀며
미리 알고 있었던 반례임에도 불구하고 검토하지 않고 맞겠거니 넘긴 것 때문에 중간에 헤맨 것 같다. 저녁 먹기 전까지 풀어보려 해서 마음이 급했다... 그리고 처음 코드가 깔끔해서 마음에 들어 구조를 변경하기 싫어서 최대한 첫 코드 구조 안에서 어떻게든 풀어보려 했는데... 이것도 시간을 쓰는데 한 몫한 것 같다. 그러지 말자..^^