[IEEE16] EIE : Efficient Inference Engine on Compressed DNN

EIE: Efficient Inference Engine on Compressed Deep Neural Network

State-of-the-art deep neural networks (DNNs) have hundreds of millions of connections and are both computationally and memory intensive, making them difficult to deploy on embedded systems with limited hardware resources and power budgets. While custom hardware helps the computation, fetching weights from DRAM is two orders of magnitude more expensive than ALU operations, and dominates the required power. Previously proposed 'Deep Compression' makes it possible to fit large DNNs (AlexNet and VGGNet) fully in on-chip SRAM. This compression is achieved by pruning the redundant connections and having multiple connections share the same weight. We propose an energy efficient inference engine (EIE) that performs inference on this compressed ne

https://arxiv.org/abs/1602.01528

Abstract (Motivation)

현대 딥러닝 모델들이 점차 구조가 복잡해지면서, 계산 비용이 높아지고 있다. Deep Compression은 Pruning과 Quantization을 통해서 정확도를 유지하면서 모델의 크기를 낮춤으로써, 계산 비용을 낮추고자 접근했던 연구이다.

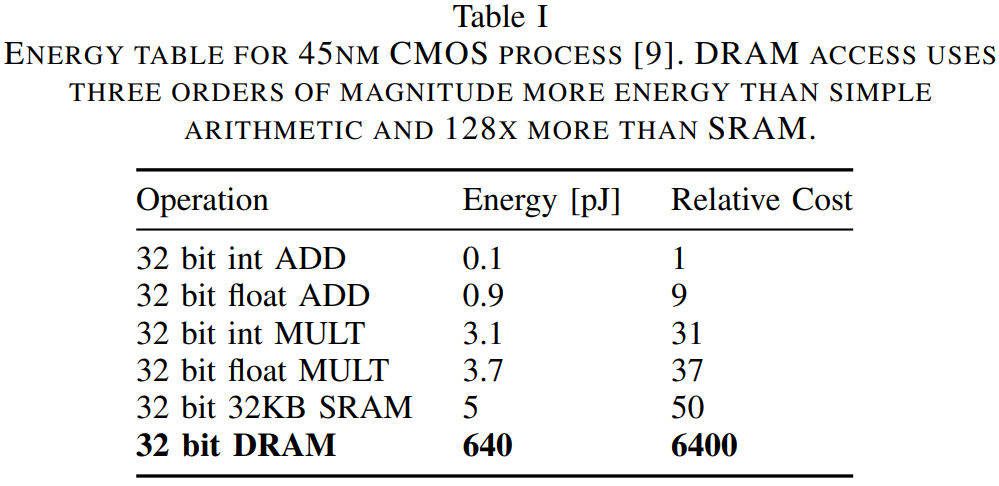
하지만 Deep Compression은 Hardware (RAM) 측면에서 한계가 존재한다. SRAM이 DRAM보다 에너지 효율성이 100배 이상 높은 반면에, Deep Compression 과정이 DRAM에서만 가능해 에너지 효율성 측면에서 한계가 존재한다는 것이다.

따라서 이 논문에서는 SRAM에서 작동하는 dynamic accerator, EIE를 통해 Hardware 측면에서 에너지 효율성을 개선했다는 점에서 의의가 있다. 이번 논문 리뷰를 통해서 Pruning, Quantization의 한계와, 왜 기존의 Deep Compression은 DRAM에서만 가능했지는지부터 시작해서, EIE의 핵심인 processing elements (PE)를 정리해보고자 한다.

Introduction

Initial Approach : Pruning

Pruning은 rebudant (불필요한) parameter를 제거함으로써 계산량을 낮추는 것이 목표인 연구 분야이다. 설명을 위해서 Magnitude based pruning을 예시로 들어보자.

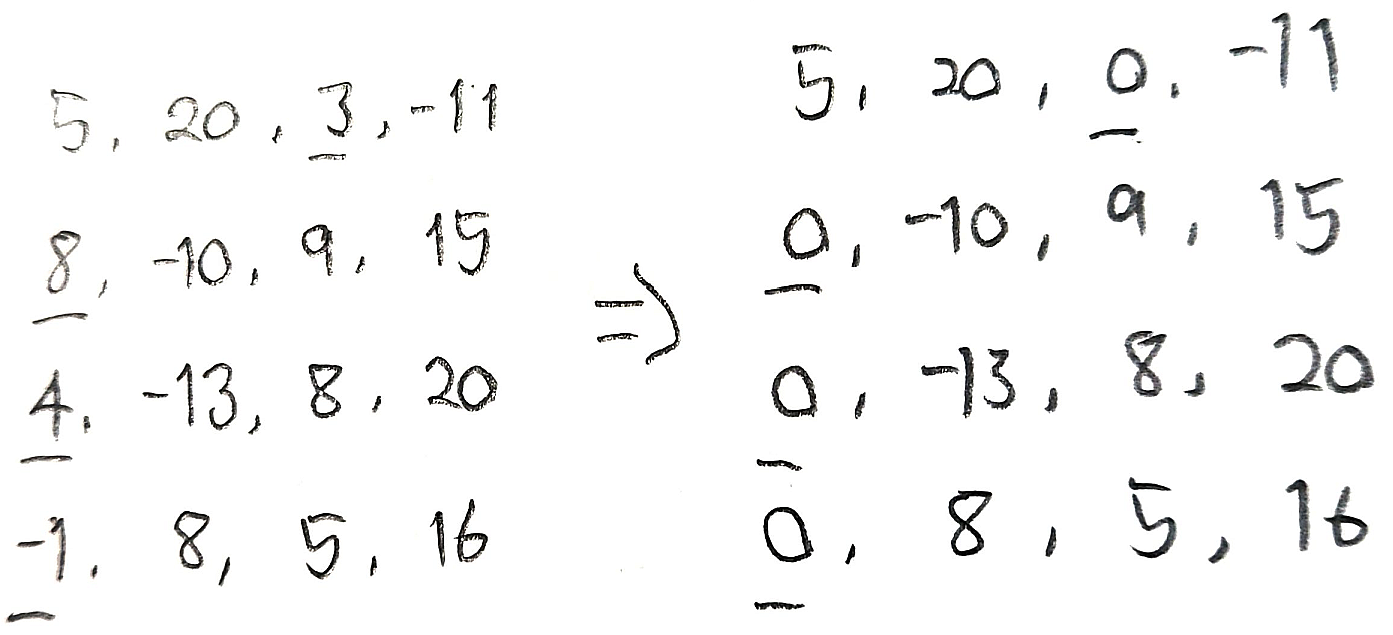
위의 사진은 4×4 Weight Matrix에 magnitude (절댓값)-based pruning을 적용하는 예시이다. [5, 20, 3, -11]에서는 3이 절댓값이 가장 작으므로 0으로 변환되고, 마찬가지로 [8, -10, 9, 15]에서는 8이, [4, -13, 8, 20]에서는 4가 0으로 변환된다.

이를 통해서 가장 중요도가 낮은 (low-magnitude) weight를 zero (0)으로 변환함으로써, 계산량을 낮춘다는 의의가 있다. 하지만 Pruning은 zero (0)의 비율이 높은, Sparse Matrix를 만들어낸다는 한계가 존재한다. 본질적인 Matrix size는 변하지 않았기 때문에, 구조적 한계가 존재한다는 것이다.

[Paper] DeepGraph : Towards Any Structural Pruning

DepGraph는 기존의 Structural Pruning에서 group-level pruning이 전체 schema를 고려하지 않기 때문에 발생하는 문제를 극복하고자 한 연구입니다.

https://until.blog/@namgyu-youn/-paper--deepgraph---towards-any-structural-pruning-rdre2g47

Initial Approach : Quantization

Basic Concept

Quantization은 bit-pattern에 대한 접근을 통해서 계산량을 낮추는 것에 주목한다. 숫자를 컴퓨터가 이해하기 위해서는 bit-pattern으로 변환하는 과정이 필요한데, 이 과정에서 quantization을 적용해 일부 mantissa (소수점)을 제거한다면, 정확도를 낮게 감소시키면서 연산량을 감소시킬 수 있다는 것이다.

예를 들어서, 12.3950216이라는 숫자가 있다고 해보자. 이 숫자를 12.395021로 변환한다면, 12.3950216 - 12.395021 = 0.0000006이라는 오차가 발생하지만, bit-pattern에서는 연샨량 감소가 유의미하기 때문에 낮은 소수점을 제거해볼 수 있다.

하지만 Quantization은 대량의 가중치들이 밀집된 layer (e.g., FC-layer)에서 취약하다는 한계가 있다. 작은 변화에도 불구하고, 전체 구조가 무너질 수도 있다는 점이다.

Solution : EIE (Efficient Inference Engine)

PE에 대해서 이야기 전에 우선, "왜 Deep Compression 과정은 DRAM에서만 가능했는가?"에 대해서 이야기할 필요가 있다. (Deep Compression에 대한 자세한 설명은 [3]에 설명되어 있으므로 생략한다.)

Initial Approach : Deep Compression

DNN 모델에 있는 다양한 layer 중에서, Hardware (RAM)에서 연산량이 가장 집중되어서 bottle-neck을 유발하는 layer는 어디일까? Transformer? Convolution? Pooling? EIE 에서는 일부 CNN 모델에서 무려 38%의 계산 시간이 FC-layer에서 발생한다고 설명한다. Layer의 특성 상 입력받은 내용을 재사용하지 않으며, 내부 구조가 모두 연결되어 있기 때문이다.

FC-layer에서 발생하는 bottle-neck을 해결하기 위해서, batch의 개념이 도입되기도 했다. 하지만 문제는, batch 특성 상 latency가 발생하기 때문에 real-time service에 적용이 어렵다는 점이다. 근본적인 문제를 해결하기 위해서 초기에 Pruning, Quantization 관련 연구들이 있었고, 그 뒤에 등장한 연구가 Deep Compression 이다.

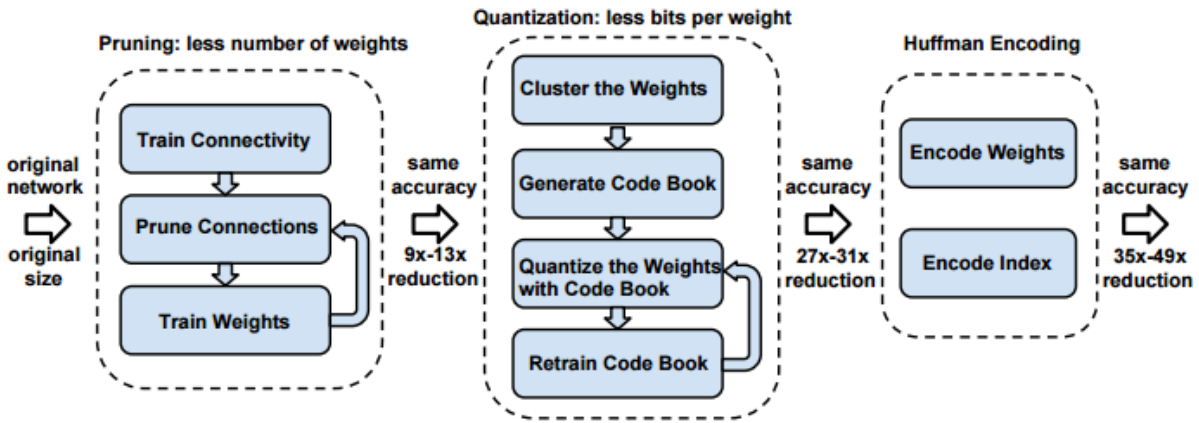
Deep Compression은 3-step (pruning -> trained quantization -> Huffman coding)을 통해서 기존의 pruning, quantization 한계점을 극복하고자 한 연구이다. 이를 통해서 sparsity를 낮추면서, 모델을 압축했으므로 bottle-neck을 해결하고자 시도했다는 점에서 의의가 있다.

하지만 Deep Compression에도 한계가 존재한다. 3-step을 통과한 결과가 irregular (불규칙) pattern이므로, SRAM에 적용할 수 없다는 것이다. 즉, 근본적인 bottle-neck 문제는 효과적으로 해결했지만, weight matrix의 내부 구조가 불규칙하기 때문에 VRAM보다 저렴한 SRAM에는 적용할 수가 없다는 한계가 존재한다.

Main Concept - PEs (Processing Elements)

PE는 Compressed DNN을 SRAM에 적용하기 위해 등장한 개념이다. (pointer에 대한 자세한 설명은 [2]를 참고해주세요)

FC-layer에서 Output Vector는 아래 사진과 같다. PE의 핵심은, W ≠ 0 and a ≠ 0 인 경우에만 연산을 하도록 구조를 변형시킨다는 점이다. 즉, 어떤 수에 0 (zero)를 곱해도 결과는 0이므로, 이 경우를 모두 생략한다는 점이다.

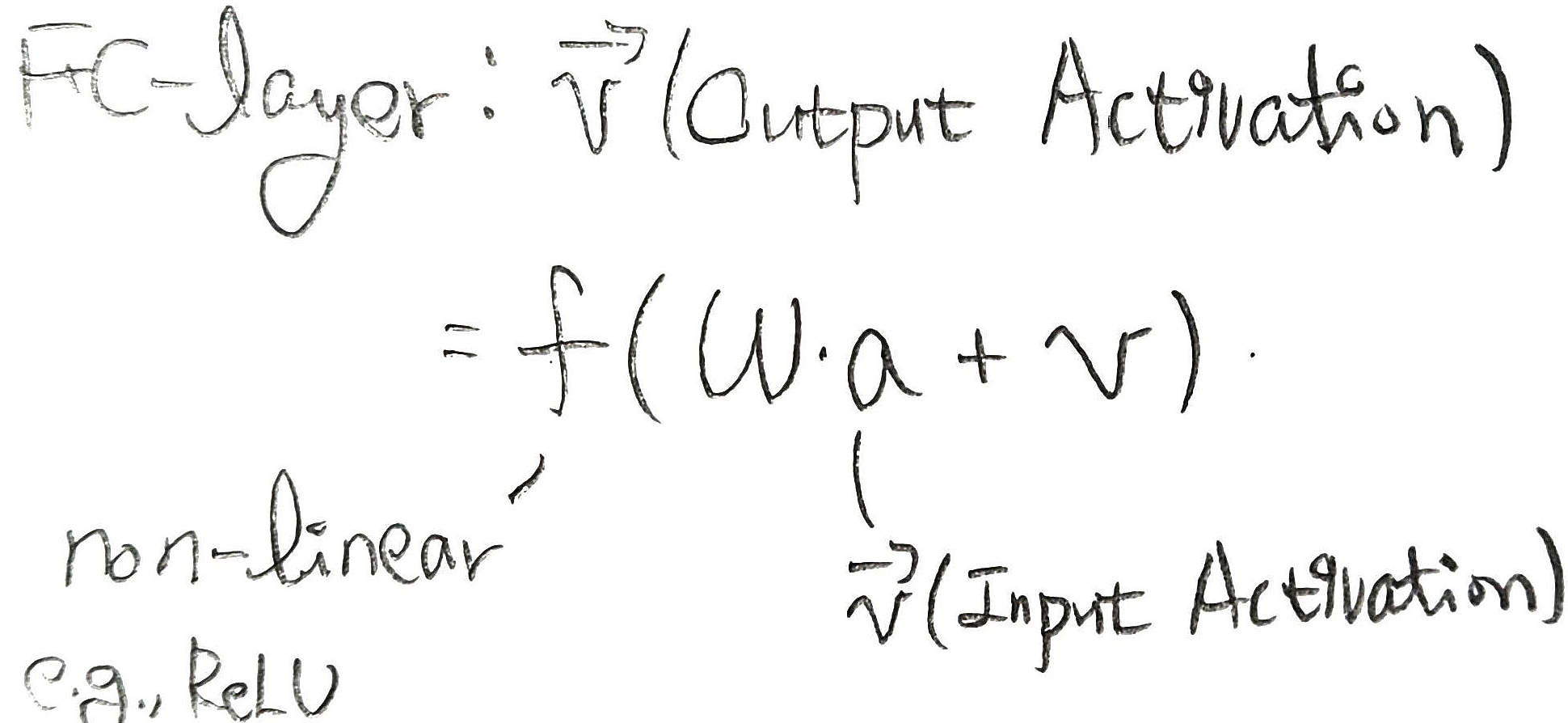
이를 위해서 (v, z, p) = (non-zero value, N(zero) before value , pointer)의 개념이 등장한다. [3]에 정말 자세한 예시가 있어서 관련 내용을 발췌했음을 밝힌다.

Representation : Example

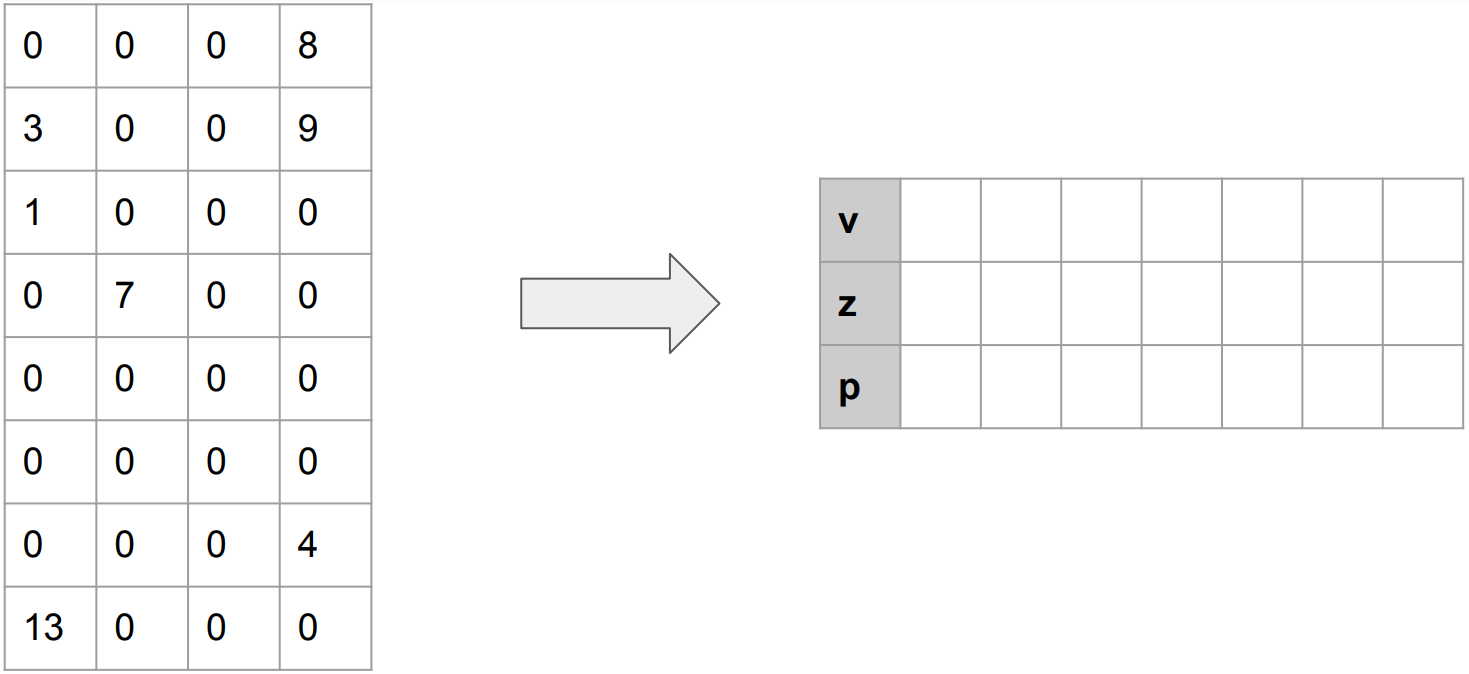
Intial Matrix (v, z, p)를 생성한다. 앞으로 진행될 과정을 통해서 Column 안에서 값을 읽으면서, (v, z, p)에 값들이 추가된다.

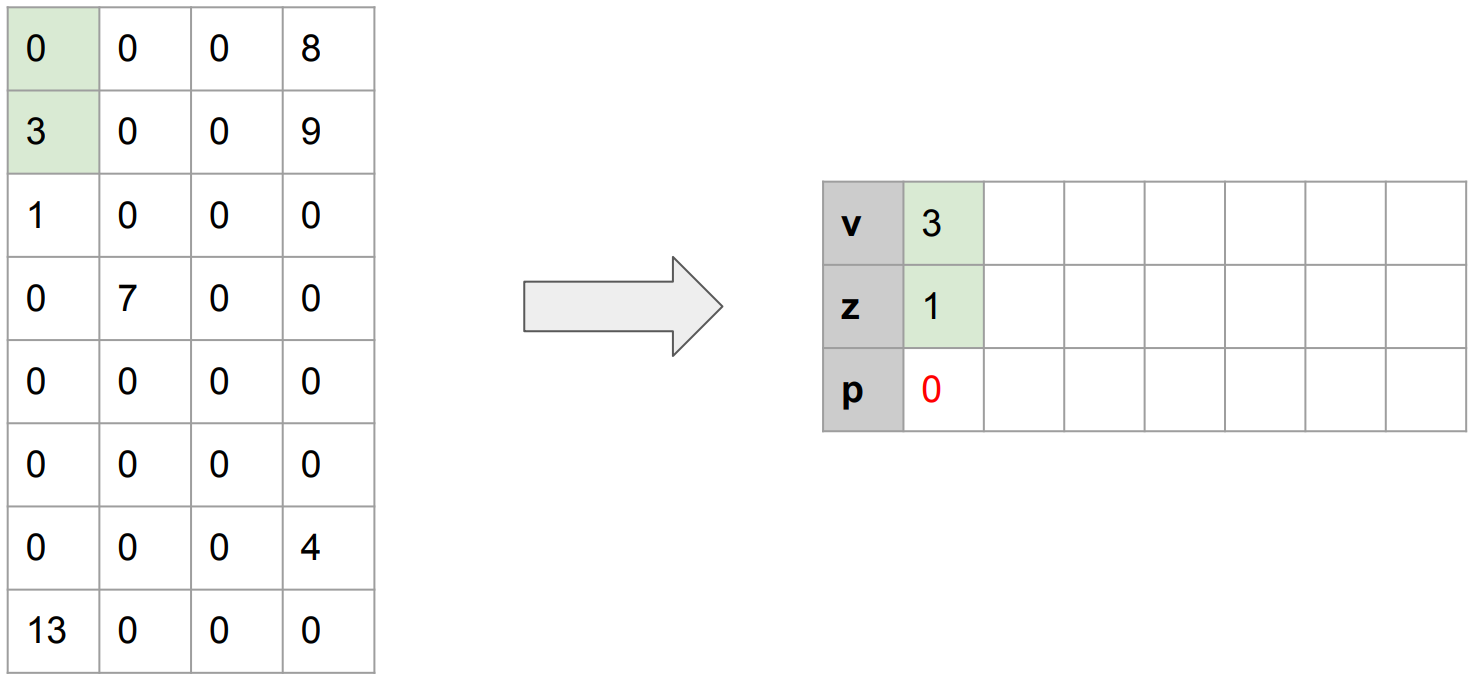
첫 번째 non-zero value (3)이 등장했다. 그렇다면 이 값을 기록해야 한다. 3 앞에는 0 (zero)가 1개 있었으므로, z에는 1이 기록된다.

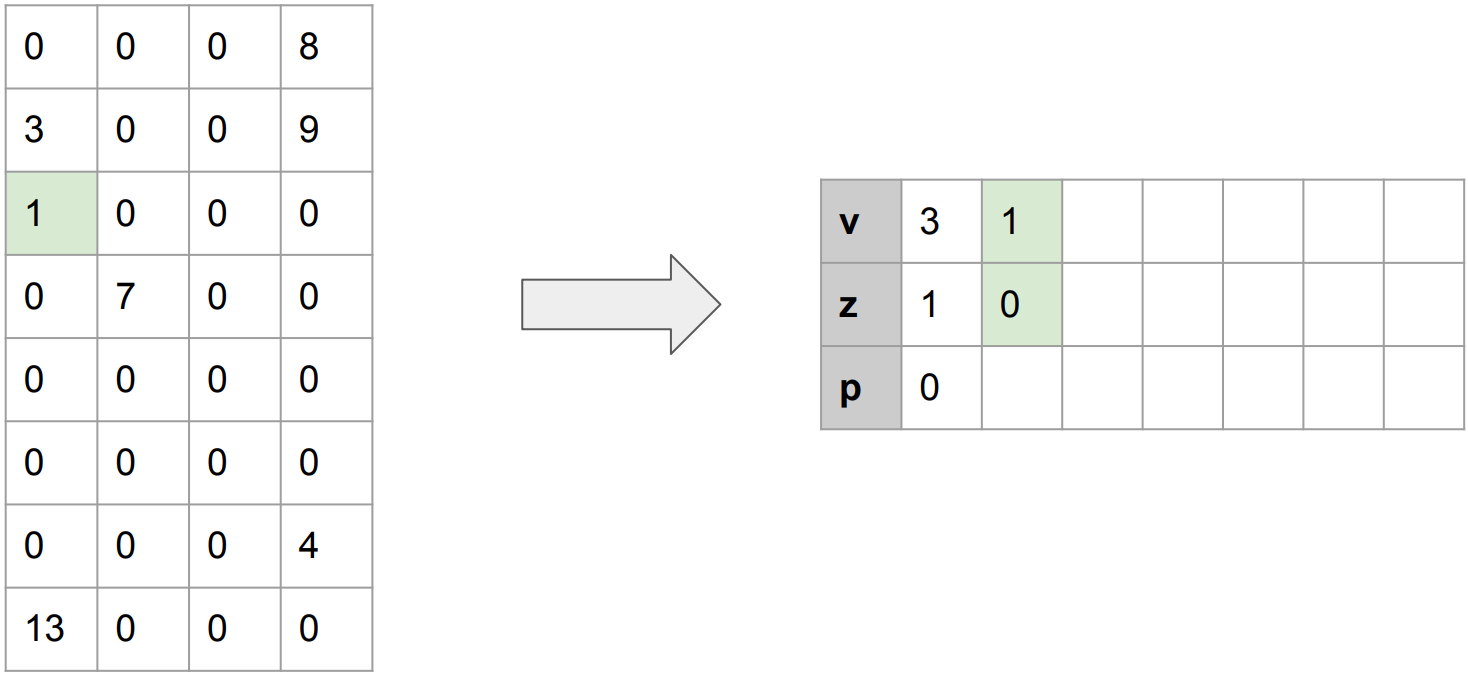
다음으로 non-zero value, 1이 등장했다. 이전에 0이 없었으므로, z에는 0이 기록된다.

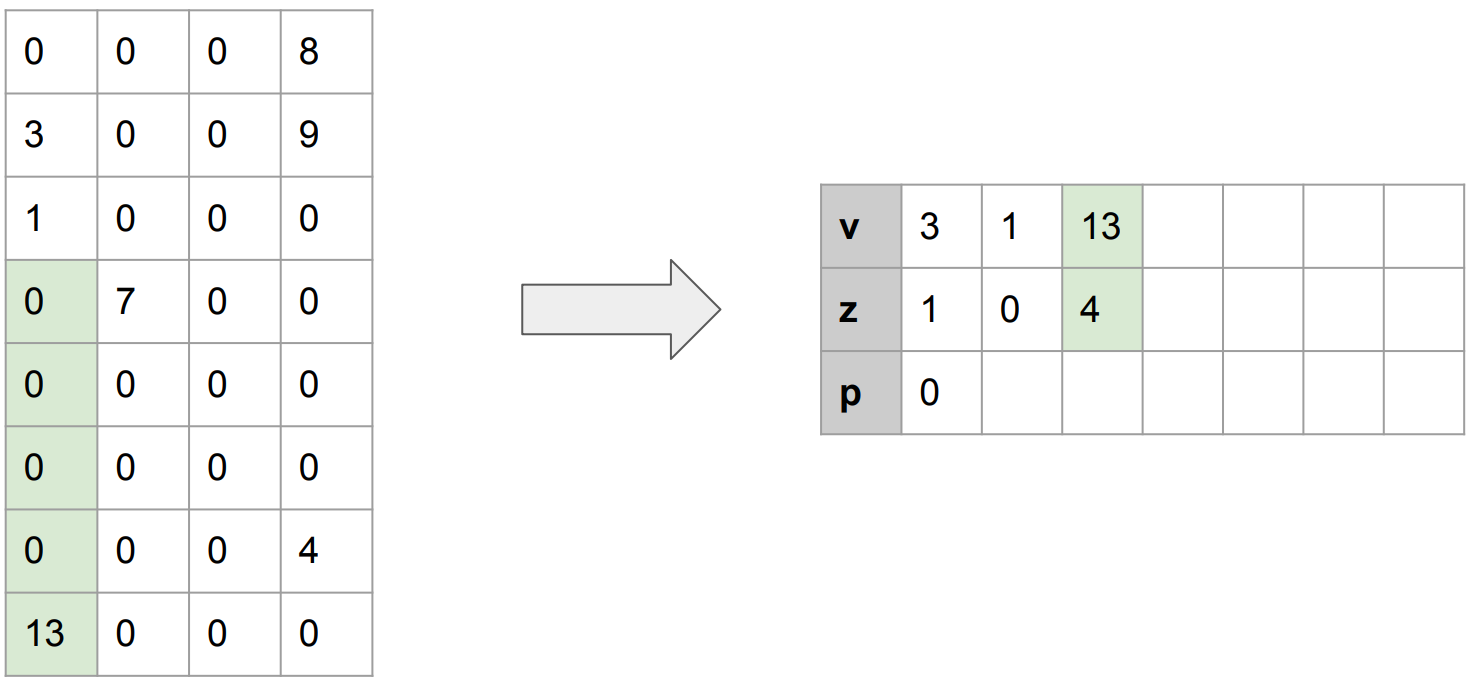
이번에는 0이 4번 있었고, 그 뒤에 13이 등장했다. 따라서 (v, z) = (13, 4)가 될 것이다.

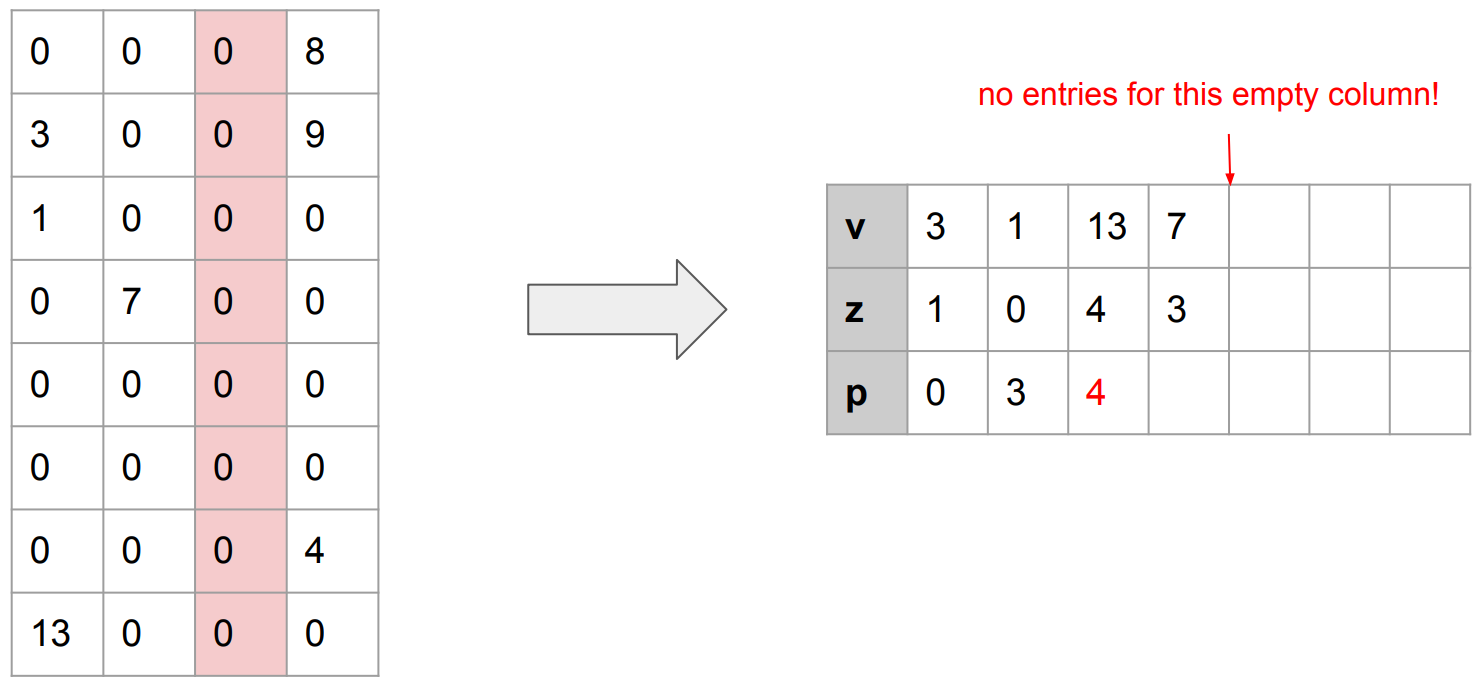
이번에는 Column 전체가 0인 상황이 발생했다. PE의 핵심은, "어떤 수에 0 (zero)를 곱해도 결과는 0이므로, 이 경우를 모두 생략한다" 였음에 주목하자. 따라서 이 경우는 하나의 Column이 생략된다.

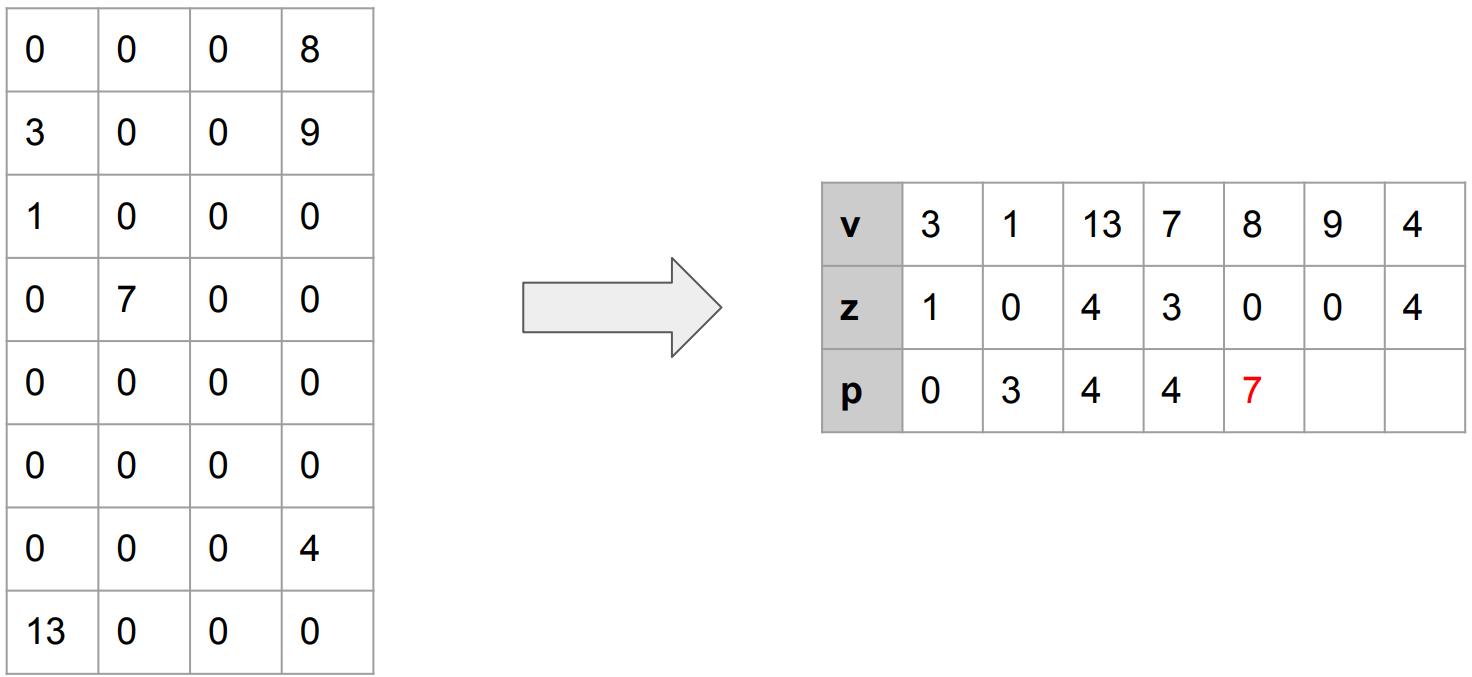
PE를 통과한 결과는 다음과 같다. 이전과 차이점은, sparsity를 유발하는 0 (zero)를 효과적으로 제거하면서, 위치 정보를 pointer를 통해 유지했다는 점이다. (Matrix size : (8, 4) -> (7, 3))

하지만 아직도 0 (zero)가 존재한다. 따라서 논문에서는 multiple-PE (=PEs)를 제안한다. PEs를 통과한 결과는 encoding되며, decoding 과정에서는 LNZD node를 통해 이전의 값을 불러와 사용한다. (See also : [2] p.29 ~ 32)

Conclusion

EIE (Efficient Inference Engine on Compressed DNN)은 기존에 연산량을 가속화하는 방법 (Deep Compression)이 있었지만, Hardware (SRAM)에 적용할 수 없다는 한계를 극복했다는 점에서 의의가 있는 연구이다. 이를 통해서 CPU 기준 24배, GPU 기준 3.4배의 에너지 효율성을 이루어 냈다는 점에서 의의가 있다.